6.Summing Amplifier

In this script, we will discuss the most important topic of Operational Amplifier, we have already discussed this topic in another script

• What is Ideal Operational Amplifier?
• Characteristics of Ideal Operational Amplifier
• Two important properties of the ideal op-amp & Math
• What is Virtual Ground 
• What is  Inverting Amplifier and Math
• Noninverting Amplifier: Voltage Follower and Math Problem

Now we will discuss

The Summing Amplifier 

The op-amp can perform addition and subtraction. The addition is performed by the summing amplifier covered in this section. The Summing Amplifier is another type of operational amplifier circuit diagram that is used to combine several inputs and produce an output that is the weighted sum of the inputs. So we can say

 " A  summing amplifier is an op-amp circuit that combines several inputs and produces an output that is the weighted sum of the  inputs"

The summing amplifier is a variation of the inverting amplifier. We post previously in the inverting operational amplifier, we saw that the inverting amplifier has a single input voltage, (Vin) applied to the inverting input terminal. It takes advantage of the fact that the inverting configuration can handle many inputs at the same time.

Summing Amplifier Equation

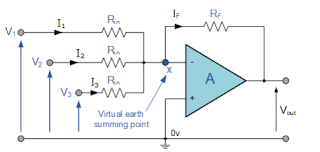
Figure: Summing Amplifier

The op-amp circuit is the summing amplifier circuit shown in the figure. The circuit shows three input v1, v2, and v3 summing amplifier circuits, which provide a means of algebraically summing three voltages, each multiplied by a constant gain factor. We keep in mind that the current entering each op-amp input is zero.

Applying the KCL node a gives

 $$i=i1+i2+i3$$

$$\frac{Va-Vo}{Rf}=\frac{V1-Va}{R1}+\frac{V2-Va}{R2}+\frac{V3-Va}{R3}$$

$$\text{We know that Va=0 }$$

$$\frac{-Vo}{Rf}=\frac{V1}{R1}+\frac{V2}{R2}+\frac{V3}{R3}$$

$$\text{[Multiplying "Rf" both side ] }$$

$$\frac{-Vo}{Rf}XRf=\frac{V1}{R1}XRf+\frac{V2}{R2}XRf+\frac{V3}{R3}XRf$$

$$Vo=-(\frac{Rf}{R1}V1+\frac{Rf}{R2}V2+\frac{Rf}{R3}V3)$$

In the words, each input adds a voltage to the output multiplied by its separate contain gain multiplier. If more inputs are used, they each add an additional component to the input.

Indicating that the output voltage is a weighted sum of the inputs. For this reason, the circuit is called summer. Needless today the summer can have more than three inputs.

Problem: 1

Find out the output voltage of an op-amp summing amplifier for the following sets of voltage and registers. Use Rf = 1MΩ  in all cases

V1=1v, V2=2v,  V3=3v, R1=500kΩ,  R2=1MΩ,  R3=1MΩ.

Solution:

$$\text{[We know that the equation is,] }$$

$$Vo=-(\frac{Rf}{R1}V1+\frac{Rf}{R2}V2+\frac{Rf}{R3}V3)$$

$$\text{[Applying the value in this equation ,] }$$

$$Vo=-(\frac{1000㏀}{500㏀}1+\frac{1000㏀}{1000㏀}2+\frac{1000㏀}{1000㏀}3)$$

$$Vo=-7v(answer)$$

Problem-2:

Calculate vo and io in the op-amp circuit in Fig.

This is summer with two inputs.

     $$Vo=-[\frac{10}{5}2+\frac{10}{2.5}1]$$

$$Vo=-8v$$

The current io is the sum of the currents through the 10-k and 2-k resistors. Both of these resistors have voltage vo= -  8 V across them,

since va =vb =  0. Hence,

$$io=-[\frac{Vo-0}{10}+\frac{Vo-0}{2}mA]$$

$$io=-4.8mA$$